GATE 1991
Question 1 |
For the digital in figure, the expression for the output f is ________

Out of syllabus. |
Question 2 |
In interleaved memory organization, consecutive words are stored in consecutive memory modules in ________ interleaving, whereas consecutive words are stored within the module in ________ interleaving.
low order, high order |
→ Consecutive words in same memory module in high order interleaving as the higher order bits determine the module.
Question 3 |
Consider the number given by the decimal expression:
163 * 9 + 162 * 7 + 16 * 5 + 3
The number of 1’s in the unsigned binary representation of the number is ________.
9 |
(9753)16
It's binary representation is,
1001011101010011
∴ The no. of 1's is 9.
Question 4 |
Using the 8087 arithmetic coprocessor with the 8087 CPU requires that the 8087 CPU is operated ________.
Out of syllabus. |
Question 5 |
When two 4-bit binary number A = a3a2a1a0 and B = b3b2b1b0 are multiplied, the digit c1 of the product C is given by _________
c1 = b1a0 ⊕ a1b0 |

⇒ c1 = b1a0 ⊕ a1b0
Question 6 |
Consider the following PASCAL program segment:
if i mode 2 = 0 then
while i > = 0 do
begin
i:=i div 2;
if i mod 2 < > 0 do then i:=i – 1
else i:=i – 2
end An appropriate loop-invariant for the while-loop is ______
PASCAL is out of syllabus. |
Question 7 |
The minimum number of comparisons required to sort 5 elements is _____
7 |
= ⌈log(n!)⌉
= ⌈log(5!)⌉
= ⌈log(120)⌉
= 7
Question 8 |
The weighted external path length of the binary tree in figure is _____

144 |
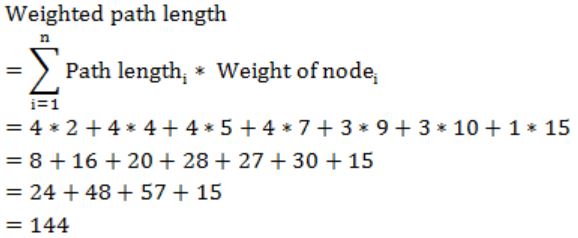
Question 9 |
If the binary tree in figure is traversed in inorder, then the order in which the nodes will be visited is ______

4, 1, 6, 7, 3, 2, 5, 8 |
(Left, Root, Right)
So, the order will be
4, 1, 6, 7, 3, 2, 5, 8
Question 10 |
Consider the following recursive definition of fib:
fib (n) : = if n = 0 then 1
else if n = 1 than 1
else fib (n – 1) + fib (n – 2) The number of times fib is called (including the first call) for an evaluation of fib (7) is ___________
41 |
T(n) = T(n-1) + T(n-2) + 2
T(0) = T(1) = 0 (for fib(0) and fib(1), there are no extra recursive calls)
T(2) = 2
T(3) = 4
T(4) = 8
T(5) = 14
T(6) = 24
T(7) = 40
Counting the initial call, we get
40+1 = 41
Question 11 |
The arithmetic expression : (a + b) * c - d / e * * f is to be evaluated on a two-address machine, where each operands, the number of registers required to evaluate this expression is ______. The number of memory access of operand is __________.
3, 4 |
So, in total 3 registers are required and 6 memory operations in total to fetch all operands.
